6.2.3 凝縮曲線と熱交換器設計
前回説明した凝縮曲線には三つの意味が含まれているのをご存じでしょうか?そしてそれは熱交換器の性能にどのような影響を与えるかを説明します。
物性の変化
一つ目は凝縮量が温度と共に変化しますので、それにより物性が大きく変わることです。つまり、流体中の液体と気体の重量比および体積比が変わること、そして液体と気体の間で物性が大きく異なることが主な理由です。例えば、溶剤として使用されるトルエンの常温(25℃)、大気圧における液体と気体の物性を比較しますと次のように液体の保有する物性値が気体に比べ大きいことがわかります。
| 物性 | 単位 | 気体 gas | 液体 liquid | liquid/gas |
| 比熱 | kJ/kg-K | 1.16 | 1.71 | 1.47 |
| 粘度 | mPa-s | 0.00712 | 0.548 | 77.0 |
| 熱伝導度 | W/m-K | 0.114 | 0.134 | 11.7 |
| 密度 | kg/m3 | 3.77 | 865 | 229.4 |
このことから凝縮量に変化により物性が大きく変わるために、境膜伝熱係数あるいは熱伝達係数が一定ではなく温度の変化により大きく変わってきます。例えば、Nusseltが次元解析で求めた管内の境膜伝熱係数hは次式表されます。

ここで各項は左からNu数、Re数、Pr数、そして管の内径と長さで作られる、いずれも無次元数です。この式のCやm,n,q等の係数は実験的に求められており、McAdamsは次式を提案しております。
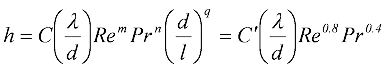
この式を使って先ほどのトルエンの物性からh:境膜伝熱係数を求めてみます。ただし、C'をMcAdamsに従って0.0225とし、dを75mm、流速dを気体で20m/s、液体で2m/sと設定します。その結果を以下に示します。
| 項目 | 単位 | 気体 gas | 液体 liquid | liquid/gas |
| Re No. | 749,242 | 236,770 | 0.298 | |
| Pr No. | 0.623 | 6.013 | 9.652 | |
| Nu No. | 977.1 | 918.9 | 0.940 | |
| 境膜伝熱係数 | kJ/m2hr-K | 621.8 | 6874.0 | 11.055 |
この結果からわかることは、
- 気体および液体の流速がそれぞれ"20m/s"および"2m/s"という標準流速の場合、液体の境膜伝熱係数が気体に比べて約11倍と大きい。つまり、熱が伝わりやすいと言うことになる。
- 液体の境膜係数がこれほど大きい理由は、それぞれのNu数がほぼ等しいことから熱伝導度の違い(liquid/gas=11.8)に依ることがわかる。
このように液体の境膜伝熱係数は気体に比べ良好である。もし、気体の伝熱係数を改善するにはどうすれば良いのであろうか。そのヒントの幾つかについて紹介する。
- 密度の改善:運転圧力を上げて気体の密度を大きくし、境膜伝熱係数を改善する。さきほどのケースでは圧力は大気圧なので、例えば20気圧程度に圧縮すると液体と同等の境膜伝熱係数となる。
- 熱伝導度の改善:トルエンには実質無理であるが、熱伝導度の大きな気体、例えばH2を混ぜることで熱伝導度を改善する。H2の熱伝導度は他の気体(N2やO2など)に比べ一桁大きい"0.17W/m-k"である。
熱量の変化
二つ目は熱量の変化です。前回お見せしました凝縮曲線にあるように、凝縮量が温度とともに変わってきますので、加熱あるいは冷却の終点温度を何度にするかで熱量が大きく変わってきます、。つまり、熱交換器に要求される伝熱負荷が変わります。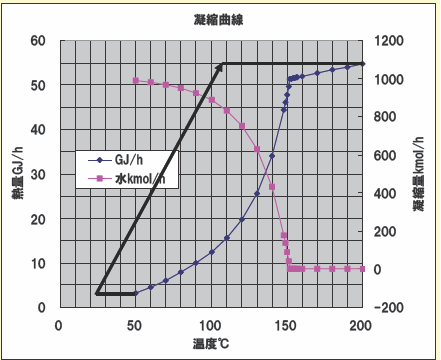
温度差の変化
熱交換器の伝熱面積は熱量を(伝熱係数×温度差)で割ることで求めることが出来ます。そのために温度差が大きければ伝熱面積は小さくなります。上図に示した熱量-温度曲線に被加熱流体でボイラ給水の変化を示しました。この太線で示したボイラ給水と加熱側である流体の温度差を見ますと直線的に変化するのではなく、ある温度を境に温度差が増加、あるいは逆に減少したりします。これが凝縮変化での特徴の一つです。るまり、伝熱面積を求める際に入口(高温端)における温度差(95℃)と出口における温度差(25℃)だけで計算すると大きな誤差を生じることがわかるでしょう。これについては詳細に別途説明いたします。
6.2.4 エンタルピーの計算
前回の「凝縮曲線の作り方」に関し、読者から質問がありましたので簡単に説明します。
流体や固体が保有する熱量(エンタルピー)は状態量と言われるように、変化する経路には関係なく求めることが出来ます。例えば、20℃の水1kgが加熱されて70℃の水1kgになる場合、水の平均比熱は1kcal/kg-Kですから保有熱量は20kcalから70kcalに増加します。その際に増加する熱量は熱量差50kcalに等しく、20℃から90℃へ上昇した後に70℃に下がったとしても、水の保有する熱量はやはり50kcalとなります。
流体が保有する熱量(エンタルピー)は圧力が一定であれば、定圧比熱Cpから容易に計算することが出来ます。その方法には平均比熱から計算する方法と、定圧比熱の積分形から計算する二つの方法があります。そこで比熱を温度の4次関数で表したとします。
比熱を温度の関数として表現する場合、より簡単な3次関数で表す場合や、"NIST webbook"のようにT^4の代わりにT^-2を使用するケースもあります。ここで使用している4次関数の係数は"Chemical Properites"を採用しております。
ここで流体をN2に設定しますと、
Cp=A+B*T+C*T^2+D*T^3+E*T^4 (J/mol-K)
ただし、A=29.342,B=-3.54E-02,C=1.01E-05,D=-4.31E-09,E=2.59E-13
平均比熱から計算する方法
基準となる温度を25℃に設定し、40℃から100℃に加熱する際の熱量の計算を行います。それぞれの温度における比熱を上式を使って計算します。まず、25℃における比熱を計算しますが、Tは絶対温度ですからTには273.15+25=298.15を代入しますと、Cp(25℃)=29.0702J/mol-Kとなります。次に40℃と100℃における比熱Cpを計算しますと、29.0918J/mol-K(@40℃)と29.2052J/mol-K(@100℃)が得られます。すると、40℃から100℃まで加熱するために必要な熱量は、
q1 = (100-25)*(Cp(25,100)-(40-25)*Cp(25,40) = 75*(29.0702+29.2052)/2-15*(29.0702+29.0918)/2 = 75*29.1377-15*29.0810 = 1749.1J/mol
比熱の積分形から計算する方法
比熱Cpの積分形、つまりエンタルピーを求めます。
∫CpdT = AT+B*T^2/2+C*T^3/2+D*T^4/4+E*T^5/5+const
次に40℃と100℃におけるエンタルピをそれぞれ計算しますと、9107.83+constと10856.53+constになりますので、その差、つまり加熱に必要な熱量は、
q2 = 10856.53+const - (9107.83+const) = 1748.70J/mol
となります。
"NIST webbook"では25℃基準のエンタルピー計算式が紹介されています。
この二つの方法から求めた熱量は、それぞれ1749.1J/molと1748.7J/molであり、その差はわずか0.02%しか過ぎませんので、平均比熱を使った計算でも実用上差し支えないものとなっています。
- 第1章 物質収支の計算
- 1.1 設計基本
- 1.2 物質収支計算ツールの準備
- 1.3 原子バランスの組み込み
- 1.4 気液分離
- 1.5 ストリームの合流(Addstream)
- 1.6 平衡定数の計算
- 1.7 平衡定数近似式の確定
- 1.8 平衡定数Kと圧平衡定数Kp
- 1.9 水蒸気改質炉出口組成計算
- 1.10 凝縮水分離とPSA水素精製
- 1.11 改質条件とCO転化条件と水素回収率への影響
- 第2章 熱収支の計算
- 2.1 熱収支計算の基礎
- 2.2 熱収支計算表の作成
- 2.3 ガス系の加熱と冷却
- 2.4 水蒸気改質炉の物質熱収支
- 2.5 予熱空気と水蒸気改質炉
- 2.6 燃焼系熱回収とスチーム発生
- 2.7 改質炉対流部プロセス設計
- 第3章 容器の設計
- 3.1 容器の種類
- 3.2 貯蔵タンク
- 3.3 分離器
- 第4章 回転機の設計
- 4.1 回転機の基礎
- 4.2 ポンプの設計
- 4.2.1 ポンプの種類と選定
- 4.2.2 ポンプのデータシート
- 4.2.2 ポンプのデータシート(流量について)
- 4.2.2 ポンプのデータシート(揚程について)
- 4.3 遠心ポンプの設計
- 4.3.1 遠心ポンプ効率の推定
- 4.3.2 遠心ポンプのNPSH
- 4.3.3 遠心ポンプのプロセス計算
- 第5章 水蒸気改質炉設計
- 5.1 改質管の設計
- 5.1.1 改質管とは
- 5.1.2 改質管の材料
- 5.1.3 Larson-Miller Parameter(LMP)
- 5.1.4 改質管の肉厚計算
- 5.2 水蒸気改質炉対流部の設計
- 5.2.1 伝熱計算
- 5.2.2 スタートアップ時の挙動
- 5.3 運転停止と水蒸気改質炉の設計
- 5.3.1 運転停止の種類
- 5.3.2 緊急停止における水蒸気改質炉
- 5.3.3 対流部熱交換器のクリープ破断
- 5.4 安全停止と改質炉設計
- 第6章 熱交換器の設計
- 6.1 熱交換器とプロセス設計
- 6.1.1 熱交換器性能とその影響
- 6.1.2 熱交換器のプロセスデータ
- 6.2 熱交換器と物性
- 6.2.1 凝縮と物性
- 6.2.2 凝縮曲線の作り方
- 6.2.3 凝縮曲線と熱交換器設計
- 6.2.4 エンタルピーの計算
- 6.2.5 凝縮熱伝達と有機溶剤
- 6.2.6 凝縮熱伝達と不凝縮ガスの影響
- 6.2.7 熱伝達と粘度の影響
- 6.2.8 熱伝達と材料の影響
- 6.3 熱交換器の選定
- 6.3.1 熱交換器の分類と種類
- 6.3.2 シェルとチューブ
- 6.3.3 熱交換器の用途とTEMA型式
- 第7章 計装制御
- 4.1 FLPT
- 4.2 圧力制御
- 4.2.1 化学プラントにおける圧力制御
- 4.2.2 圧縮機吸込側の圧力制御システム
- 4.2.3 圧縮機吸込側の圧力調節弁の容量
- 4.2.4 圧力上昇の要因
- 4.2.5 Closed outlet



 前のページへ
前のページへ