熱交換器、凝縮、凝縮曲線、蒸発潜熱、蒸気圧

designpractice220.gif

この”プロセス設計の実務”では、プラントエンジニアリングの基幹となるプロセス設計の”イロハ”について説明しており、プラントエンジニアリングやプロセスエンジニアリングに興味がある社会人や学生を対象にしています。

この”プロセス設計の実務”では、基本に帰って「プロセス設計とは？」をもう少し掘り下げていきたいと考えています。その進め方については以下のように考えています。

  1. 「天然ガスを原料とする水素製造プラントのプロセス設計」を例題として設定いたします。
  2. プロセス設計というよりは基本設計＋詳細設計の一部を含めた範囲としますので、機器設計や配管設計などに言及することが多くなります。
  3. 実際の設計に使用するエンジニアリング・ツールなどを使用しながら説明いたします。
  4. 更新のインターバルは原則として週１回（月曜日）と考えていますが、他のテーマを優先することもあります。

6. 熱交換器の設計

6.2 熱交換器と物性
6.2.2 凝縮曲線の作り方

凝縮曲線、すなわちコンデンシング・カーブ（condensing curve）は混相状態における熱交換器の設計に不可欠な物性の一つで、その中に含まれている情報は、

  1. 熱交換器入口および出口における気液比（モル比あるいは重量比）と組成、ならびに気液それぞれの物性（密度または分子量、比熱、熱伝導率、粘度）
  2. 熱交換器入口～出口までの分割された区間における気液比（モル比あるいは重量比）と組成、ならびに気液それぞれの物性（密度または分子量、比熱、熱伝導率、粘度）
  3. 熱交換器入口～出口間での凝縮または蒸発の開始温度（露点または沸点）
  4. 熱交換器入口～出口間での気液それぞれの熱量と、入口と出口の熱量差（すなわち交換熱量）

単相における熱交換器と異なり、伝熱現象が異なるために多くの情報を必要とします。
この凝縮曲線を作成するためには、入口～出口までの分割された区間における各物質の蒸気圧が必要となります。ここでは説明を簡単にするために対象とする流体を空気とスチームの混合気体とします。その入口出口における流量や組成およびスチームの蒸気圧、そしてエンタルピを下記に示します。（エンタルピは25℃基準としています）
なお、圧力（全圧）は1.0MPaで空気流量および水蒸気＋水流量はそれぞれ1000kmol/hとします。また、各温度における水蒸気流量は次式から計算しています。

水蒸気流量 = 空気流量×蒸気圧／（全圧－蒸気圧）

温度 蒸気圧 エンタルピkJ/kg 流量kmol/h
℃ MPa 水蒸気 －水－ 水蒸気 －水－ 水蒸気+水 空気
0 0.0006 2396.1 -104.9 0.6 999.4 1000.0 1000.0
20 0.0023 2432.6 -20.9 2.3 997.7 1000.0 1000.0
40 0.0074 2468.7 62.7 7.4 992.6 1000.0 1000.0
60 0.0199 2504.0 146.3 20.4 979.6 1000.0 1000.0
80 0.0474 2538.2 230.1 49.8 950.2 1000.0 1000.0
100 0.1014 2570.7 314.3 112.9 887.1 1000.0 1000.0
120 0.1987 2601.1 398.9 247.9 752.1 1000.0 1000.0
140 0.3615 2628.6 484.4 566.2 433.8 1000.0 1000.0
150 0.4761 2641.1 527.4 908.8 91.2 1000.0 1000.0
160 0.6181 2662.5 570.7 1000.0 0.0 1000.0 1000.0
180 1.0026 2707.6 658.3 1000.0 0.0 1000.0 1000.0
200 1.5547 2751.1 747.6 1000.0 0.0 1000.0 1000.0

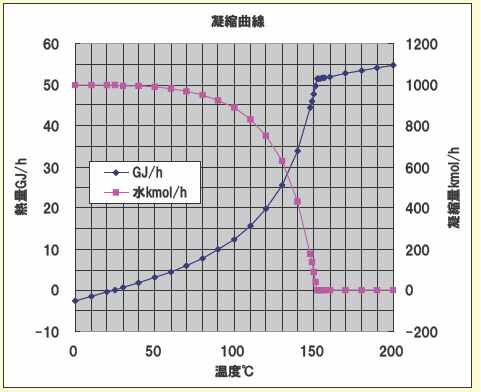
この表から水蒸気および水のエンタルピと流量を掛けて熱量を計算します。さらに空気のエンタルピ（kJ/kg or kJ/kmol）を求め、同じく空気の熱量を計算します。次に先ほどの水蒸気と水の熱量を合計し、横軸に温度をとってプロットすれば凝縮曲線を求めることができます。その結果を下図に示しました。また、横軸に温度、縦軸に水の流量をプロットすれば凝縮量の推移を見ることが出来ます。

熱量 = 水蒸気流量×水蒸気エンタルピ＋水流量×水エンタルピ＋空気流量×空気エンタルピ

なお、露点付近（150℃）では温度区間を細かくすることにより、凝縮曲線の変化が良くわかるようになります。

HX12.png

hint&blue002.gif

エンタルピー計算の基礎

流体や固体が保有する熱量は状態量と言われるように、変化する経路には関係なく求めることが出来ます。例えば、20℃の水1kgが加熱されて70℃の水1kgになる場合、水の平均比熱は1kcal/kg-Kですから保有熱量は20kcalから70kcalに増加します。その際に増加する熱量は熱量差50kcalに等しく、20℃から90℃へ上昇した後に70℃に下がったとしても、水の保有する熱量はやはり50kcalとなります。

流体が保有する熱量（エンタルピー）は圧力が一定であれば、定圧比熱Cpから容易に計算することが出来ます。その方法には平均比熱から計算する方法と、定圧比熱の積分形から計算する二つの方法があります。そこで比熱を温度の関数で表したとします。また流体をN2に設定しますと、

Cp=A+B*T+C*T^2+D*T^3+E*T^4 (J/mol-K)
ただし、A=29.342,B=-3.54E-02,C=1.01E-05,D=-4.31E-09,E=2.59E-13

平均比熱から計算する方法

基準となる温度を25℃に設定し、40℃から100℃に加熱する際の熱量の計算を行います。それぞれの温度における比熱を上式を使って計算します。まず、25℃における比熱を計算しますが、Tは絶対温度ですからTには273.15+25=298.15を代入しますと、Cp(25℃)=29.0702J/mol-Kとなります。次に40℃と100℃における比熱Cpを計算しますと、29.0918J/mol-K（@40℃）と29.2052J/mol-K（@100℃）が得られます。すると、40℃から100℃まで加熱するために必要な熱量は。

q1 = (100-25)*(Cp(25,100)-(40-25)*Cp(25,40) = 75*(29.0702+29.2052)/2-15*(29.0702+29.0918)/2 = 75*29.1377-15*29.0810 = 1749.1J/mol

比熱の積分形から計算する方法

比熱Cpの積分形、つまりエンタルピーを求めます。
∫CpdT = AT+B*T^2/2+C*T^3/2+D*T^4/4+E*T^5/5+const
次に40℃と100℃におけるエンタルピをそれぞれ計算しますと、9107.83+constと10856.53+constになりますので、その差、つまり加熱に必要な熱量は、

q2 = 10856.53+const - (9107.83+const) = 1748.70J/mol

となります。

この二つの方法から求めた熱量は、それぞれ1749.1J/molと1748.7J/molであり、その差はわずか0.02%しか過ぎませんので、平均比熱を使った計算でも実用上差し支えないものとなっています。