ベルヌーイの定理

バスタブに貯まっているお湯を抜くと、最初は液面が急激に低下しますが、その後、次第に液面の低下速度が遅くなっていきます。では、バスタブに貯まっていたお湯を全量抜くためにはどれだけの時間がかかるでしょうか？
この計算をするためにはベルヌーイの定理を利用します。つまり、液高さというポテンシャルエネルギーとバスタブの栓からお湯が流出する時の速度エネルギーを考慮します。

化学プラントでタンク内の液を抜き出すために最初はポンプで液を移送し、液面がポンプ吸込配管より低下した後は、別のドレンノズルからグラビティでタンク内の液を半地下ピットなどに回収します。
この液の抜き出しにどれだけの時間がかかるでしょうか？　もし、ドレンノズルから抜き出す時間が1日もかかるようだと、その後の作業スケジュールに大きく影響します。
このベルヌーイの定理を使えば、容器の底または壁から流体が噴出する際の速度は液高さから計算することが出来ます。ここで容器の大きさが十分に大きく、液高さが一定値Ho[m]とし、容器底の穴高さが高さの基準面、つまり、高さZ=0とすれば、穴からの噴出する際の理論速度Vは次式で計算出来ます。

ただし、穴から噴出する際に圧力損失を伴いますので、その影響を速度係数Cvで表しますと次式となります。

また、穴から噴出する際には噴出する流体の断面積は穴の断面積より小さくなり、これを縮流現象と言います。この断面積の比を縮流係数Ccで表現し、先ほどの速度係数Cvとの積を流出係数Cd、穴の断面積をA[m2]とすれば、流出する流量は次式で計算します。

液面降下時間と流速計算

変数	項目	単位	数値
H	初期液面高さ	mm
h	終了液面高さ	mm
D	ドラム内径	mm
d	穴径	mm
Cd	流出係数	-
計算結果
time	降下時間	sec
V(initial)	初期流出速度	m/sec
V(setting)	終了流出速度	m/sec

使い方

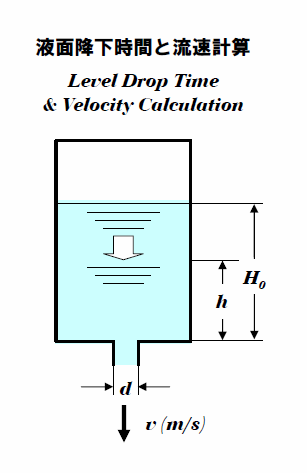
H（初期液面高さ）、h（終了液面高さ）、D（槽直径）、d（穴径）の数値欄に入力し、
"calculation"ボタンをクリックすれば、液面が初期高さから終了高さまでの降下時間と、
各高さにおける流出速度の計算結果が表示されます。

一部の数値を変更してやり直す場合には、再入力後に
"calculation"ボタンをクリックして再計算して下さい。

注意事項

（１）流出係数は初期設定で0.6にしていますが、変更は可能です。
（２）流出速度の計算には流出係数（Cd）に代わりに速度係数(Cv)を使うのですが、
　　ここではCdを使用しています。なお、Cd = Cv×Cc（縮流係数）です。

ドラムに溜まっている液が下部の穴から流出する際の、
初期の液面Hからhに降下するまでに要する時間と、
Hおよびhにおける流出速度を計算します。

降下時間の計算式は、

time = 1/Cd×(D/d)^2×(2/2g)×（H^0.5－h^0.5）

また、流出速度は、

v = Cv×（2g×h）^0.5