1.4 流動

化学プラントは点と線から構成されています。この点に相当するのが機器や装置で、線に相当するのが機器を結ぶ配管や電気ケーブルあるいは計装空気配管などです。この「流動」は機器や配管内の流体の状況を把握するために必要な「単位操作」で、機械系であれば流体工学として知られている工学理論体系です。
流体が流れるとそこに摩擦によるエネルギー損失を生じます。それが配管内では圧力損失として現れ、それを補うために圧縮機やポンプなどの流体機械が使われます。つまり、「流動」は配管内の摩擦損失（圧力損失）を計算して、必要となる流体機械の仕様を決定し、そこで消費されるエネルギーを最適化するために配管口径を決める際に役に立つ化学工学の「単位操作」です。

1.4.1 流動と拡散

この「拡散」は分子レベルの移動のことで、例えば工場の煙突から排出される分子の拡散や、今、話題となっている放射能汚染はこの「拡散」という移動現象により説明が可能です。
流動の基本式の一つは粘性と摩擦に関するはニュートンの粘性法則です。ご存じのように流体の流れの様式には層流と乱流があります。層流とは一言で言えば流れがゆったりとした状態のことで、例えば水道の蛇口をゆっくりとひねって行くと、最初に現れる一筋の半透明な流れが層流です。次第に蛇口を開けていくと水の流れが速くなり、周辺の空気を巻き込んで色は白くなります。これが乱流です。

流体は種類や状態に応じて異なった粘性を有しており、これを粘性係数μで表現しています。また、粘性がない流体を完全流体あるいは理想流体と呼んでいますが、この完全流体は超流動現象などで見られる以外存在せず、流体工学の理論展開において導入された概念です。
この層流では流体間で粘性に起因する摩擦力が働きます。この摩擦力は流体の運動量の時間的変化として見なすことが出来、ニュートンの粘性法則では以下のように表現されています。

流れの剪断力τは粘性係数μと速度勾配du/dxに比例する。ただし、粘性係数が速度勾配に依存しない流れをニュートン流体と言い、依存するような流れを非ニュートン流体と言う。

このニュートンの粘性法則とフイックの法則およびフーリエの法則として知られている式は、それぞれ物質、運動量および熱の移動（拡散）を示しています。

このフーリエの法則とニュートンの粘性法則を変形しますと、上記３式の係数の次元は全て[m2/sec]となり、これらは物質、熱、運動量の拡散係数となります。特にニュートンの粘性法則のμ/ρは動粘性係数あるいは動粘度として知られています。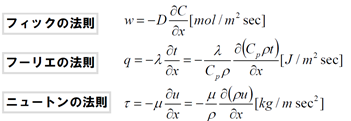

この単位[cm2/s]はストークス（Stokes）と呼ばれています

次回はこの圧力損失の計算と層流と乱流について話すことにします。

次回に続く・・・。